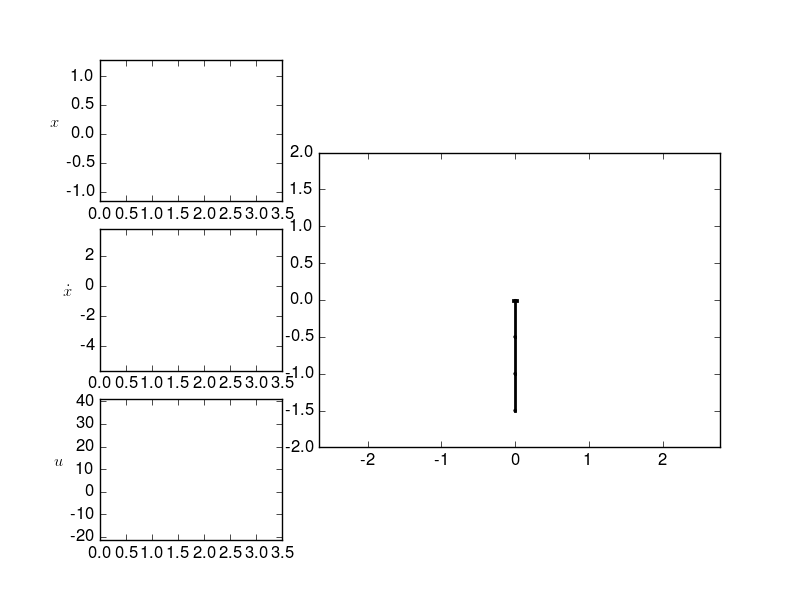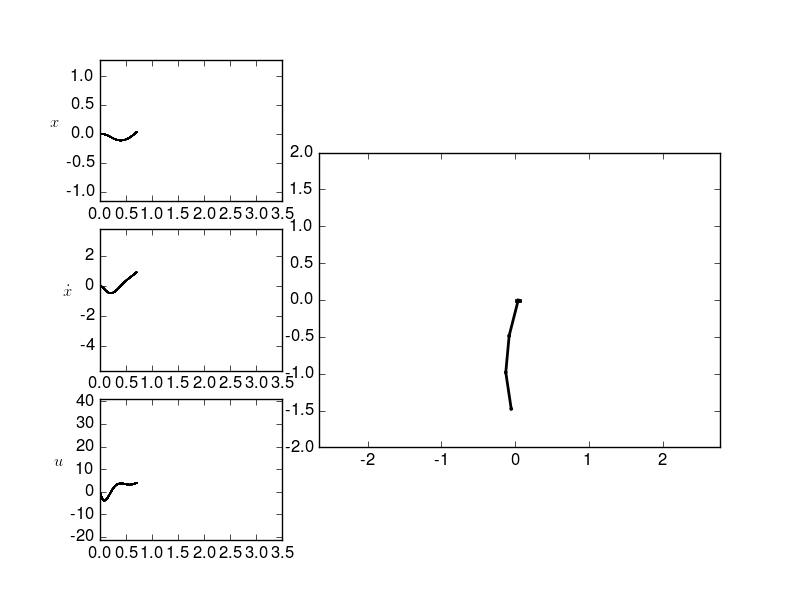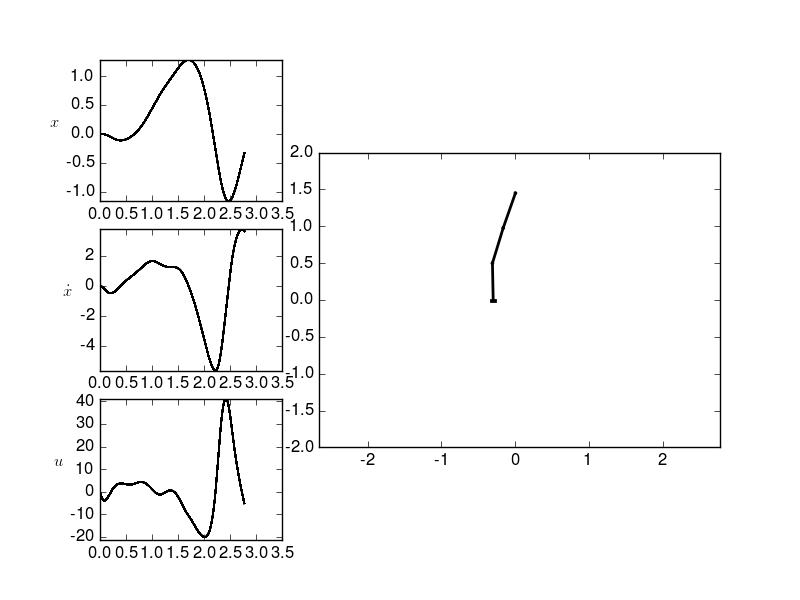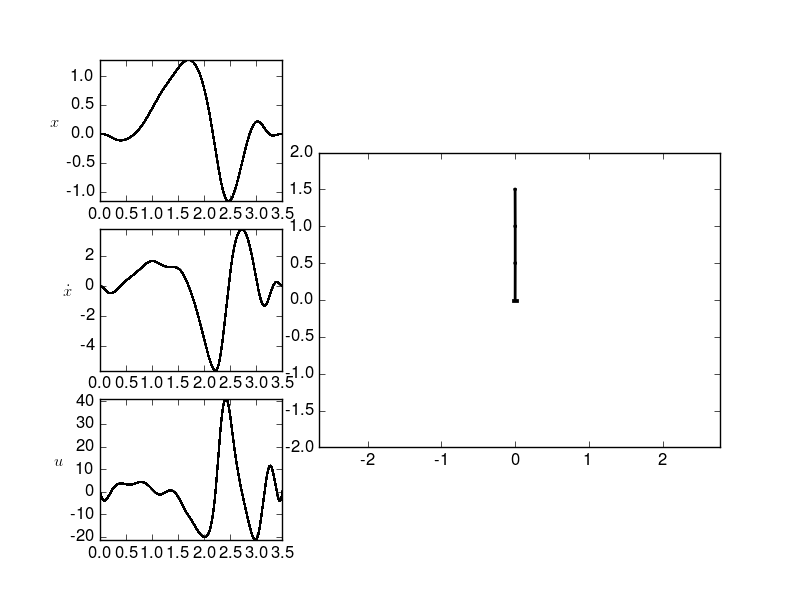
Swing up of a 3-bar pendulum¶
Now we consider a cart with 3 pendulums attached to it.
To get a callable function for the vector field of this dynamical system we need to set up and solve its motion equations for the accelaration.
Therefore, the function n_bar_pendulum generates the mass matrix
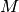and right hand site 
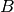of the motion equations 
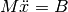for a general 
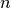-bar pendulum, which we use for the case 
.
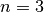The formulas this function uses are taken from the project report ‘Simulation of the inverted pendulum’ written by C. Wachinger, M. Pock and P. Rentrop at the Mathematics Departement, Technical University Munich in December 2004.
Source Code¶
# 3-bar pendulum
# import all we need for solving the problem
from pytrajectory import ControlSystem
import numpy as np
import sympy as sp
from sympy import cos, sin
from numpy import pi
def n_bar_pendulum(N=1, param_values=dict()):
'''
Returns the mass matrix :math:`M` and right hand site :math:`B` of motion equations
.. math::
M * (d^2/dt^2) x = B
for the :math:`N`\ -bar pendulum.
Parameters
----------
N : int
Number of bars.
param_values : dict
Numeric values for the system parameters,
such as lengths, masses and gravitational acceleration.
Returns
-------
sympy.Matrix
The mass matrix `M`
sympy.Matrix
The right hand site `B`
list
List of symbols for state variables
list
List with symbol for input variable
'''
# first we have to create some symbols
F = sp.Symbol('F') # the force that acts on the car
g = sp.Symbol('g') # the gravitational acceleration
m = sp.symarray('m', N+1) # masses of the car (`m0`) and the bars
l = sp.symarray('l', N+1)#[1:] # length of the bars (`l0` is not needed nor used)
phi = sp.symarray('phi', N+1)#[1:] # deflaction angles of the bars (`phi0` is not needed nor used)
dphi = sp.symarray('dphi', N+1)#[1:] # 1st derivative of the deflaction angles (`dphi0` is not needed nor used)
if param_values.has_key('F'):
F = param_values['F']
elif param_values.has_key(F):
F = param_values[F]
if param_values.has_key('g'):
g = param_values['g']
elif param_values.has_key(g):
g = param_values[g]
else:
g = 9.81
for i, mi in enumerate(m):
if param_values.has_key(mi.name):
m[i] = param_values[mi.name]
elif param_values.has_key(mi):
m[i] = param_values[mi]
for i, li in enumerate(l):
if param_values.has_key(li.name):
l[i] = param_values[li.name]
elif param_values.has_key(li):
l[i] = param_values[li]
C = np.empty((N,N), dtype=object)
S = np.empty((N,N), dtype=object)
I = np.empty((N), dtype=object)
for i in xrange(1,N+1):
for j in xrange(1,N+1):
C[i-1,j-1] = cos(phi[i] - phi[j])
S[i-1,j-1] = sin(phi[i] - phi[j])
for i in xrange(1,N+1):
if param_values.has_key('I_%d'%i):
I[i-1] = param_values['I_%d'%i]
#elif param_values.has_key(Ii):
# I[i] = param_values[Ii]
else:
I[i-1] = 4.0/3.0 * m[i] * l[i]**2
#-------------#
# Mass matrix #
#-------------#
M = np.empty((N+1, N+1), dtype=object)
# 1st row
M[0,0] = m.sum()
for j in xrange(1,N):
M[0,j] = (m[j] + 2*m[j+1:].sum()) * l[j] * cos(phi[j])
M[0,N] = m[N] * l[N] * cos(phi[N])
# rest of upper triangular part, except last column
for i in xrange(1,N):
M[i,i] = I[i-1] + (m[i] + 4.0*m[i+1:].sum()) * l[i]**2
for j in xrange(i+1,N):
M[i,j] = 2.0*(m[j] + 2.0*m[j+1:].sum())*l[i]*l[j]*C[j-1,i-1]
# the last column
for i in xrange(1,N):
M[i,N] = 2.0*(m[N]*l[i]*l[N]*C[N-1,i-1])
M[N,N] = I[N-1] + m[N]*l[N]**2
# the rest (lower triangular part)
for i in xrange(N+1):
for j in xrange(i,N+1):
M[j,i] = 1 * M[i,j]
#-----------------#
# Right hand site #
#-----------------#
B = np.empty((N+1), dtype=object)
# first row
B[0] = F
for j in xrange(1,N):
B[0] += (m[j] + 2.0*m[j+1:].sum())*l[j]*sin(phi[j]) * dphi[j]**2
B[0] += (m[N]*l[N]*sin(phi[N])) * dphi[N]**2
# rest except for last row
for i in xrange(1,N):
B[i] = (m[i] + 2.0*m[i+1:].sum())*g*l[i]*sin(phi[i])
for j in xrange(1,N):
B[i] += (2.0*(m[j] + 2.0*m[j+1:].sum())*l[j]*l[i]*S[j-1,i-1]) * dphi[j]**2
B[i] += (2.0*m[N]*l[N]*l[N]*S[N-1,i-1]) * dphi[N]**2
# last row
B[N] = m[N]*g*l[N]*sin(phi[N])
for j in xrange(1,N+1):
B[N] += (2.0*m[N]*l[j]*l[N]*S[j-1,N-1]) * dphi[j]**2
# build lists of state and input variables
x, dx = sp.symbols('x, dx')
state_vars = [x, dx]
for i in xrange(1,N+1):
state_vars.append(phi[i])
state_vars.append(dphi[i])
input_vars = [F]
# return stuff
return sp.Matrix(M), sp.Matrix(B), state_vars, input_vars
def solve_motion_equations(M, B, state_vars=[], input_vars=[], parameters_values=dict()):
'''
Solves the motion equations given by the mass matrix and right hand side
to define a callable function for the vector field of the respective
control system.
Parameters
----------
M : sympy.Matrix
A sympy.Matrix containing sympy expressions and symbols that represent
the mass matrix of the control system.
B : sympy.Matrix
A sympy.Matrix containing sympy expressions and symbols that represent
the right hand site of the motion equations.
state_vars : list
A list with sympy.Symbols's for each state variable.
input_vars : list
A list with sympy.Symbols's for each input variable.
parameter_values : dict
A dictionary with a key:value pair for each system parameter.
Returns
-------
callable
A callable function for the vectorfield.
'''
M_shape = M.shape
B_shape = B.shape
assert(M_shape[0] == B_shape[0])
# at first we create a buffer for the string that we complete and execute
# to dynamically define a function and return it
fnc_str_buffer ='''
def f(x, u):
# System variables
%s # x_str
%s # u_str
# Parameters
%s # par_str
# Sympy Common Expressions
%s # cse_str
# Vectorfield
%s # ff_str
return ff
'''
###########################################
# handle system state and input variables #
###########################################
# --> leads to x_str and u_str which show how to unpack the variables
x_str = ''
u_str = ''
for var in state_vars:
x_str += '%s, '%str(var)
for var in input_vars:
u_str += '%s, '%str(var)
x_str = x_str + '= x'
u_str = u_str + '= u'
############################
# handle system parameters #
############################
# --> leads to par_str
par_str = ''
for k, v in parameters_values.items():
# 'k' is the name of a system parameter such as mass or gravitational acceleration
# 'v' is its value in SI units
par_str += '%s = %s; '%(str(k), str(v))
# as a last we remove the trailing '; ' from par_str to avoid syntax errors
par_str = par_str[:-2]
# now solve the motion equations w.r.t. the accelerations
# (might take some while...)
#print " -> solving motion equations w.r.t. accelerations"
# apply sympy.cse() on M and B to speed up solving the eqs
M_cse_list, M_cse_res = sp.cse(M, symbols=sp.numbered_symbols('M_cse'))
B_cse_list, B_cse_res = sp.cse(B, symbols=sp.numbered_symbols('B_cse'))
# solve abbreviated equation system
#sol = M.solve(B)
Mse = M_cse_res[0]
Bse = B_cse_res[0]
cse_sol = Mse.solve(Bse)
# substitute back the common subexpressions to the solution
for expr in reversed(B_cse_list):
cse_sol = cse_sol.subs(*expr)
for expr in reversed(M_cse_list):
cse_sol = cse_sol.subs(*expr)
# use SymPy's Common Subexpression Elimination
#cse_list, cse_res = sp.cse(sol, symbols=sp.numbered_symbols('q'))
cse_list, cse_res = sp.cse(cse_sol, symbols=sp.numbered_symbols('q'))
################################
# handle common subexpressions #
################################
# --> leads to cse_str
cse_str = ''
#cse_list = [(str(l), str(r)) for l, r in cse_list]
for cse_pair in cse_list:
cse_str += '%s = %s; '%(str(cse_pair[0]), str(cse_pair[1]))
# add result of cse
for i in xrange(M_shape[0]):
cse_str += 'q%d_dd = %s; '%(i, str(cse_res[0][i]))
cse_str = cse_str[:-2]
######################
# create vectorfield #
######################
# --> leads to ff_str
ff_str = 'ff = ['
for i in xrange(M_shape[0]):
ff_str += '%s, '%str(state_vars[2*i+1])
ff_str += 'q%s_dd, '%(i)
# remove trailing ',' and add closing brackets
ff_str = ff_str[:-2] + ']'
############################
# Create callable function #
############################
# now we can replace all placeholders in the function string buffer
fnc_str = fnc_str_buffer%(x_str, u_str, par_str, cse_str, ff_str)
# and finally execute it which will create a python function 'f'
exec(fnc_str)
# now we have defined a callable function that can be used within PyTrajectory
return f
# we consider the case of a 3-bar pendulum
N = 3
# set model parameters
l1 = 0.25 # 1/2 * length of the pendulum 1
l2 = 0.25 # 1/2 * length of the pendulum 2
l3 = 0.25 # 1/2 * length of the pendulum 3
m1 = 0.1 # mass of the pendulum 1
m2 = 0.1 # mass of the pendulum 2
m3 = 0.1 # mass of the pendulum 3
m = 1.0 # mass of the car
g = 9.81 # gravitational acceleration
I1 = 4.0/3.0 * m1 * l1**2 # inertia 1
I2 = 4.0/3.0 * m2 * l2**2 # inertia 2
I3 = 4.0/3.0 * m2 * l2**2 # inertia 3
param_values = {'l_1':l1, 'l_2':l2, 'l_3':l3,
'm_1':m1, 'm_2':m2, 'm_3':m3,
'm_0':m, 'g':g,
'I_1':I1, 'I_2':I2, 'I_3':I3}
# get matrices of motion equations
M, B, state_vars, input_vars = n_bar_pendulum(N=3, param_values=param_values)
# get callable function for vectorfield that can be used with PyTrajectory
f = solve_motion_equations(M, B, state_vars, input_vars)
# then we specify all boundary conditions
a = 0.0
xa = [0.0, 0.0, pi, 0.0, pi, 0.0, pi, 0.0]
b = 3.5
xb = [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]
ua = [0.0]
ub = [0.0]
# now we create our Trajectory object and alter some method parameters via the keyword arguments
S = ControlSystem(f, a, b, xa, xb, ua, ub, constraints=None,
eps=4e-1, su=30, kx=2, use_chains=False,
use_std_approach=False)
# time to run the iteration
x, u = S.solve()