Underactuated Manipulator¶
In this section, the model of an underactuated manipulator is treated.
The system consists of two bars with the mass 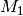 and
and
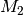 which are connected to each other via the joint
which are connected to each other via the joint 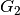 .
The angle between them is designated by
.
The angle between them is designated by 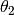 . The joint
. The joint
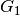 connects the first rod with the inertial system, the angle
to the
connects the first rod with the inertial system, the angle
to the 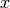 -axis is labeled
-axis is labeled 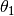 .
In the joint
.
In the joint 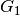 the actuating torque
the actuating torque 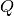 is applied. The
bars have the moments of inertia
is applied. The
bars have the moments of inertia 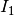 and
and 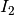 . The
distances between the centers of mass to the joints are
. The
distances between the centers of mass to the joints are 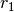 and
and
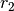 .
.

The modeling was taken from the thesis of Carsten Knoll
(April, 2009) where in addition the inertia parameter 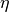 was
introduced.
was
introduced.
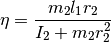
For the example shown here, strong inertia coupling was assumed with
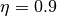 . By partial linearization to the output
. By partial linearization to the output 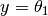 one obtains the state representation with the states
one obtains the state representation with the states
![x = [\theta_1, \dot{\theta}_1, \theta_2, \dot{\theta}_2]^T](../../_images/math/6da61fe06c2df2463181a37044965c25e76f0e9d.png) and
the new input
and
the new input 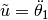 .
.
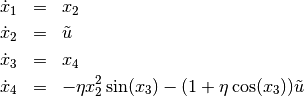
For the system, a trajectory is to be determined for the transfer
between two equilibrium positions within an operating time of
![T = 1.8 [s]](../../_images/math/de54e9885ba8acb1b3187f17ccdd191539a5b832.png) .
.
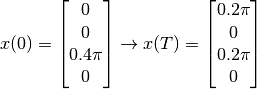
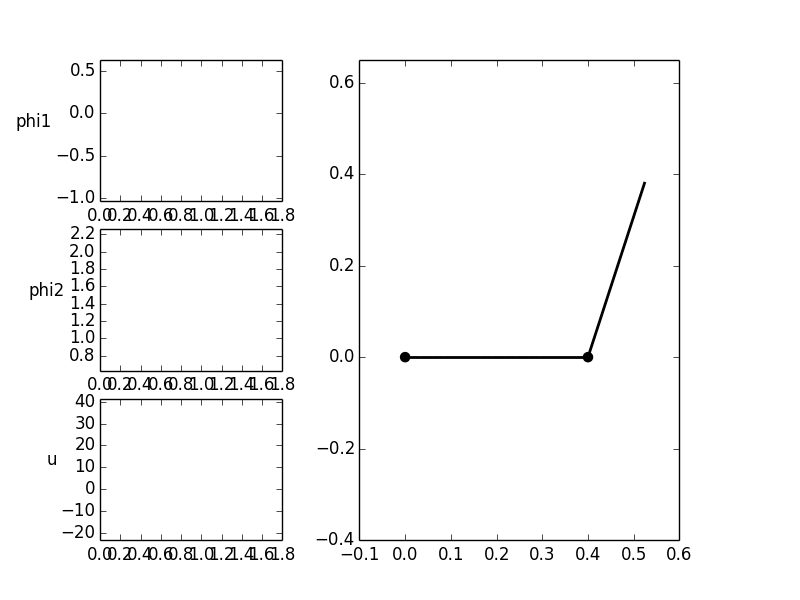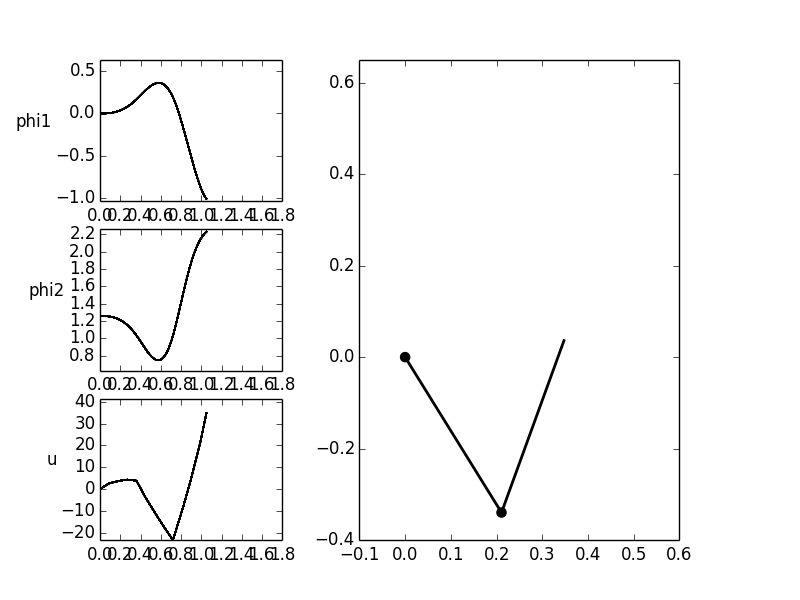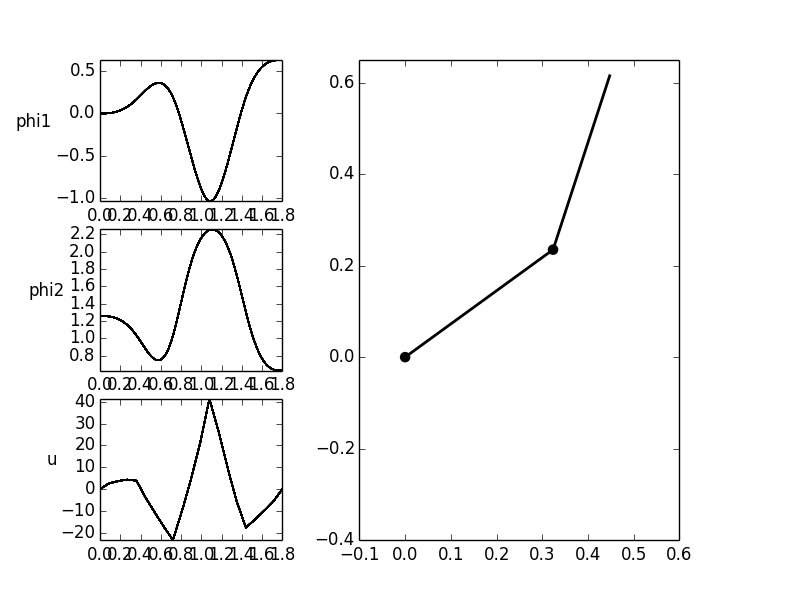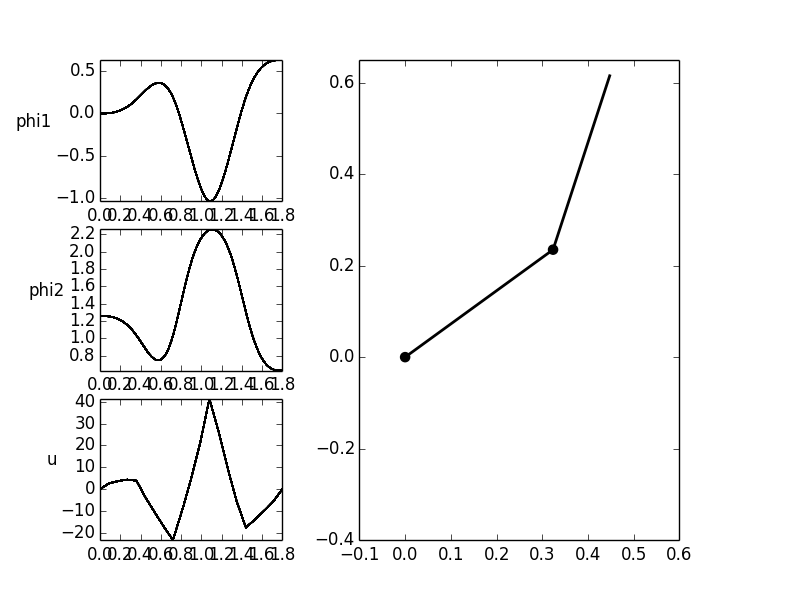
The trajectory of the inputs should be without cracks in the transition
to the equilibrium positions ( ).
).
Source Code¶
# underactuated manipulator
# import trajectory class and necessary dependencies
from pytrajectory import ControlSystem
import numpy as np
from sympy import cos, sin
# define the function that returns the vectorfield
def f(x,u):
x1, x2, x3, x4 = x # state variables
u1, = u # input variable
e = 0.9 # inertia coupling
s = sin(x3)
c = cos(x3)
ff = np.array([ x2,
u1,
x4,
-e*x2**2*s-(1+e*c)*u1
])
return ff
# system state boundary values for a = 0.0 [s] and b = 1.8 [s]
xa = [ 0.0,
0.0,
0.4*np.pi,
0.0]
xb = [ 0.2*np.pi,
0.0,
0.2*np.pi,
0.0]
# boundary values for the inputs
ua = [0.0]
ub = [0.0]
# create trajectory object
S = ControlSystem(f, a=0.0, b=1.8, xa=xa, xb=xb, ua=ua, ub=ub)
# also alter some method parameters to increase performance
S.set_param('su', 20)
S.set_param('kx', 3)
# run iteration
S.solve()